Applications

Generate sequences

Once we have a trained model, we can use it to generate new sequences. This can be done using the command:

  $ ./adabmDCA.sh sample -p <path_params> -d <fasta_file> -o <output_folder> --ngen <num_gen>

where output_folder is the directory where to save the data and num_gen is the number of sequences to be generated. The routine will first compute the mixing time (\(t^{\mathrm{mix}}\)) of the model by running a simulation starting from the sequences of the input MSA. After that, it will randomly initialize num_gen Markov chains and run for nmix \(\cdot t^{\mathrm{mix}}\) sweeps to ensure that the model equilibrates. It will save in the output directory a FASTA file containing the sequences sampled with the model and a text file containing the records used to determine the convergence of the algorithm. Figure mixing time-Right shows the comparison between the entries of the covariance matrices obtained from the data and from the generated sequences. The Pearson correlation coefficient is the same used as a target for the training and the slope is close to 1, meaning that the model is able to correctly recover the two-sites statistics of the data MSA.

Convergence criterium

To determine the convergence of the Monte Carlo simulation, the following strategy is used. We extract \texttt{nmeasure}\(=N\) sequences from the data MSA according to their statistical weight and we make a copy of them. The first set represents the chains simulated up to time \(t\), and we denote them as \(\pmb{A}(t) = \{\pmb{a}_1(t), \dots, \pmb{a}_{N}(t)\}\), while the sequences of the second set are the chains simulated until time \(t/2\), and we call them \(\pmb{A}(t/2) = \{\pmb{a}_1(t/2), \dots, \pmb{a}_{N}(t/2)\}\). With some abuse of notation, we define the intrachain correlation and autocorrelation as

\[ \mathrm{SeqID}(t) = \frac{1}{N} \sum_{i=1}^{N} \mathrm{SeqID}(\pmb{a}_i(t), \pmb{a}_{\sigma(i)}(t)) \qquad \mathrm{SeqID}(t, t/2) = \frac{1}{N} \sum_{i=1}^{N} \mathrm{SeqID}(\pmb{a}_i(t), \pmb{a}_i(t/2)) \]

where \(\sigma(i)\) is a random permutation of the index \(i\) and

\[ \mathrm{SeqID}(\pmb{a}, \pmb{b}) = \frac{1}{L}\sum_{i=1}^L \delta_{a_i, b_i} \in [0, 1] \]

is the normalized sequence identity (or overlap) between the sequences \(\pmb{a}\) and \(\pmb{b}\). By construction, at the initialization we have \(\mathrm{SeqID}(t, t/2) = 1\) and \(\mathrm{SeqID}(t)\) somewhat close to the average sequence identity of the MSA. The convergence is obtained when chains are mixed, meaning that the system has completely forgotten the initial configuration. This requirement is satisfied when the statistics of a set of independent chains is the same as the one between the initialization and the evolved chains, meaning \(\mathrm{SeqID}(t) \cong \mathrm{SeqID}(t, t/2)\). The point at which the two curves merge is called mixing time, and we denote it as \(t^{\mathrm{mix}}\). After reaching the mixing time of the model, the algorithm will initialize ngen chains at random. It will run a sampling for other nmix \(\cdot t^{\mathrm{mix}}\) steps to guarantee complete thermalization, with nmix=2 by default. Together with the generated sequences, the script will output a text file containing the records of \(\mathrm{SeqID}(t)\) and \(\mathrm{SeqID}(t, t/2)\) and their standard deviations (figure mixing time-Left).

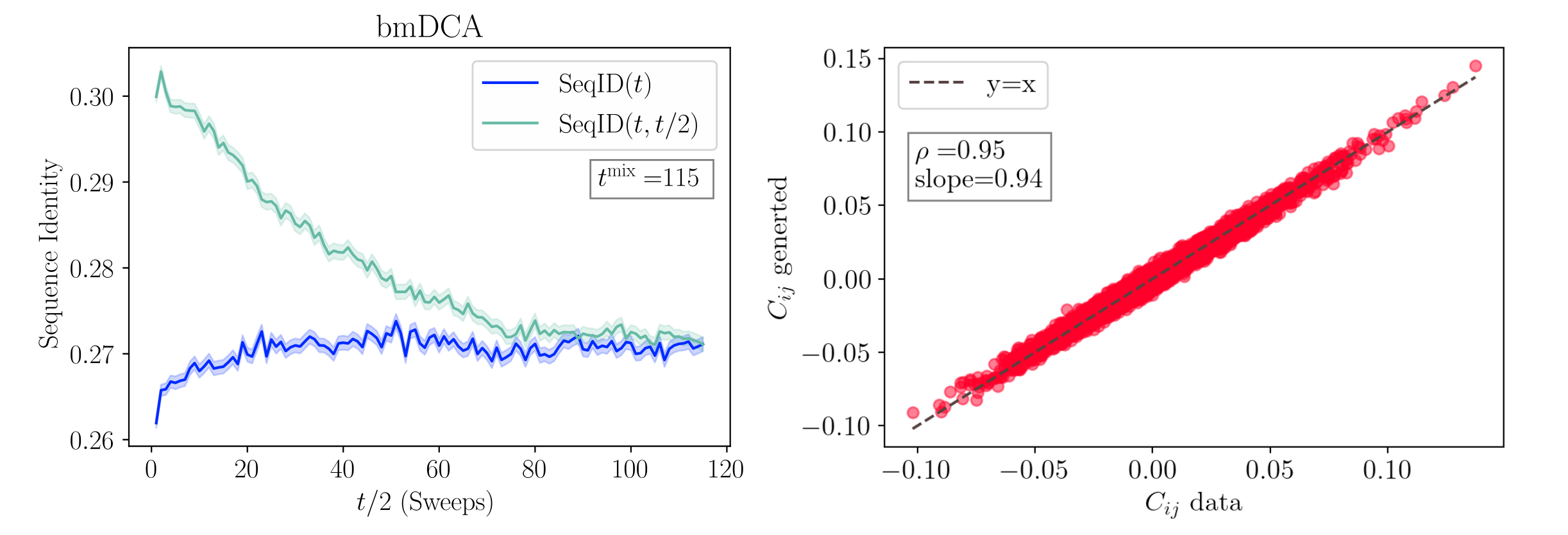
Analysis of a bmDCA model. Left: measuring the mixing time of the model using \(10^4\) chains. The curves represent the average overlap among randomly initialized samples (dark blue) and the one among the same sequences between times \(t\) and \(t/2\) (light blue). Shaded areas represent the error of the mean. When the two curves merge, we can assume that the chains at time \(t\) forgot the memory of the chains at time \(t/2\). This point gives us an estimate of the model’s mixing time, \(t^{\mathrm{mix}}\). Notice that the times start from 1, so the starting conditions are not shown. Right: Scatter plot of the entries of the Covariance matrix of the data versus that of the generated samples.

Contact prediction

One of the principal applications of the DCA models has been that of predicting a tertiary structure of a protein or RNA domain. In particular, with each pair of sites \(i\) and \(j\) in the MSA, adabmDCA 2.0 computes a contact score that quantifies how likely the two associated positions in the chains are in contact in the three-dimensional structure. Formally, it corresponds to the average-product corrected (APC) Frobenius norms of the coupling matrices [Ekeberg et al., 2013], i.e.

(1)\[ F_{i,j}^{\rm APC} = F_{i,j} - \frac{\sum_{k} F_{i,k} \sum_{k} F_{k,j}}{\sum_{kl} F_{k,l}}, \quad F_{i,j} = \sqrt{\sum_{a,b \neq `-`} J_{i,j}\left(a, b \right)^{2}} \]

Note that the coupling parameters are usually transformed in a zero-sum gauge before computing the scores, and the gap symbol should be neglected while computing the sum in Eq. (1) [Feinauer et al., 2014]. The scores for all site pairs are provided in the output folder in a separate file called <label>_frobenius.txt The first two columns indicate the site indices and the third one contains the associated APC Frobenius norm. The command for computing the matrix of Frobenius norms is

$ ./adabmDCA.sh contacts -p <file_params>  -o <output_folder>

Scoring a sequence set

At convergence, users can score a set of input sequences according to a trained DCA model by using the command line

  $ ./adabmDCA.sh energies -d <fasta_file>  -p <file_params>  -o <output_folder>

adabmDCA 2.0 will produce a new FASTA file in the output folder <output_folder> where the input sequences in <fasta_file> have an additional field in the name that account for the DCA energy function computed according to the model in <file_params>. Note that low energies correspond to good sequences.

Single mutant library

Another possible application exploits the sequence-fitness score computable according to the energy function \(E\) in Eq. (1). This routine provides a single-mutant library for a given wild type to possibly guide Deep Mutational Scanning (DMS) experiments. In particular, adabmDCA 2.0 allows one to predict the fitness reduction (increase) in terms of \(\Delta E = E\left(\rm mutant \right) - E\left(\rm wildtype \right)\) for positive (negative) value of \(\Delta E\), respectively [Hopf et al., 2017]. To produce a FASTA file containing all weighted single-mutants one has to run

  $ ./adabmDCA.sh DMS -d <WT> -p <file_params> -o <output_folder>

where <WT> is the name of the FASTA file containing the wild type sequence, <file_params> is a model file in a format compatible with adabmDCA 2.0 output, and <output_folder> corresponds to the folder that will contain the library file. The sequences in the output FASTA file are named after the introduced mutation and the corresponding \(\Delta E\); for instance, >G27A | DCAscore: -0.6 denotes that position 27 has been changed from G to A and \(\Delta E = -0.6\).